Z-transform

過去我曾發過一篇文章討論 PID Controller 的離散形式，當時在抱怨大學的控制課沒有教到 PID 的離散版，導致我們在控制板上實作 PID 控制時不知道該怎麼下手。實際上離散版本的控制理論是一門研究所的課叫做數位控制，因為數位電腦是為離散的系統，訊號進入電腦處理前都會經過取樣，是為離散訊號，當訊號為離散時，很多原本套用在連續訊號上的分析不再有效，例如說 Laplace transform，因此我們需要針對離散訊號討論其系統描述和控制器設計。

Z-transform 是 Laplace transform 的離散版本，如果懂 Laplace 的話，Z-transform 不過就是把連續的訊號先離散化之後再使用 Laplace 轉換。

因此在談論 Z-transform 之前需要知道怎麼將連續訊號離散化。

Time Sampling

首先定義取樣間距 $T_s$，即每隔 $T_s$ 單位時間取樣一次

Credit

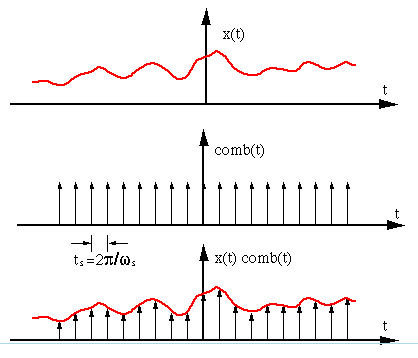
我們可以用以下數學式表達取樣後的訊號

$$x_s(t) = x(t) \sum^\infty_{k=-\infty} \delta(t-kT_s)$$

其中 $x$ 為原始訊號，$x_s$ 為取樣後的訊號，$\Sigma \delta$ 為 impulse train function (上圖中間的函數)，即在取樣點有值，其餘為零的函數，$k$ 為第 $k$ 個取樣點。

因為除了取樣點以外都為零，非取樣點的訊號並不影響，且 Laplace 轉換只關心零點以後的訊號，我們可以將方程式改寫為

$$x_s(t) = \sum^\infty_{k=0} x(kT_s) \delta(t-kT_s)$$

Z-transform

將離散化的訊號取 Laplace 轉換
$$ \begin{equation} \begin{split} \mathcal{L}\{x_s(t)\} = X_s(s) &= \int^\infty_0 [\sum^\infty_{k=0} x(kT_s) \delta(t-kT_s)] e^{-st} dt \\ &= \sum^\infty_{k=0} x(kT_s) \int^\infty_0 \delta(t-kT_s) e^{-st} dt \\ &= \sum^\infty_{k=0} x(kT_s) e^{-kT_ss} \end{split} \end{equation} $$

設 $z=e^{sT_s}, x[k]=x(kT_s)$，我們可以得到

$$ \mathcal{Z}\{x(t)\}=\mathcal{L}\{x_s(t)\}=\sum^\infty_{k=0} x[k] z^{-k} $$

即課本中常見的 Z-transform 公式，是不是很好理解呢？因此只需要記得 Z-transform 是訊號離散化的 Laplace transform 就行了。